Q. There are five persons P, Q, R, S and T each one of whom has to be assigned one task. Neither P nor Q can be assigned Task-1. Task-2 must be assigned to either R or S. In how many ways can the assignment be done?

Explanation : 

There are 5 tasks and 5 persons p q r s t

There are 5 tasks to be assigned to 5 people.

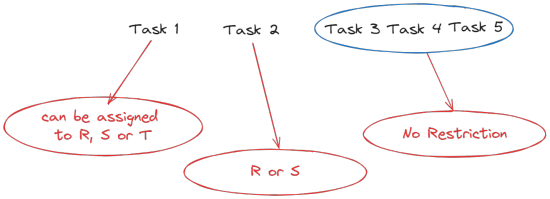
Task-1 cannot be assigned to P or Q. So, it can be assigned to R, S or T in 3 ways.

Task-2 must be assigned to either R or S. If Task-1 was assigned to R or S, then Task-2 can only be assigned to the remaining person. If Task-1 was assigned to T, then Task-2 can be assigned to either R or S. So, Task-2 can be assigned in 2 ways.

The remaining 3 tasks can be assigned to the remaining 3 people in 3! = 6 ways.

So, the total number of ways to assign the tasks is 3 * 2 * 6 = 24.