CSAT 2023

Q. ABCD is a square. One point on each of AB and CD; and two distinct points on each of BC and DA are chosen. How many distinct triangles can be drawn using any three points as vertices out of these six points?

(a) 16
(b) 18
(c) 20
(d) 24
Correct Answer: (c) 20

Question from UPSC Prelims 2023 CSAT

Explanation :

ABCD square. Points on sides AB, CD, BC, DA.

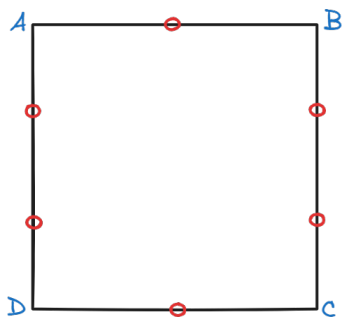
The total number of ways to choose 3 points out of 6 is given by the combination formula C(n, r) = n! / [r!(n-r)!], where n is the total number of items, r is the number of items to choose, and “!” denotes factorial.

So, the total number of triangles is C(6, 3) = 6! / [3!(6-3)!] = 20.

Check Demo Video

More Questions:

Q. A rectangular floor measures 4 m in length and 2.2 m in breadth. Tiles of size 140 cm by 60 cm have to be laid such that the tiles do not overlap. A tile can be placed in any orientation so long as its edges are parallel to the edges of the floor. What is the maximum number of tiles that can be accommodated on the floor?

Q. To encourage research is one of the functions of a university.

Q. The paradox of choice is illustrated by the story of Buridan’s ass. Jean Buridan, the 14th century philosopher, wrote about free will and the inability to choose due to numerous choices and uncertainties.

Q. In an economic organization, allowing mankind to benefit by the productivity of machines should lead to a very good life of leisure, and much leisure is apt to be tedious except to those who have intelligent activities and interests. If a leisured population is to be happy, it must be an educated population. and must be educated with a view to enjoyment as well as to the direct usefulness of technical knowledge.

Q. A study conducted on the impacts of climate change over the Cauvery basin of Tamil Nadu using regional climate models showed an increasing trend for maximum and minimum temperatures, and a decrease in the number of rainy days.