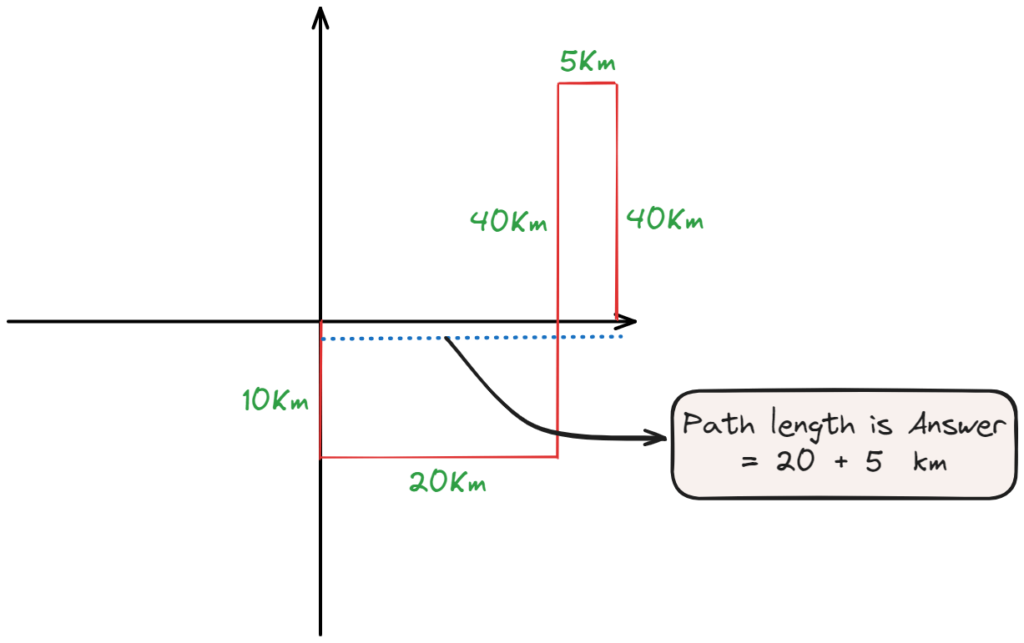
Q. A bank employee drives 10 km towards South from her house and turns to her left and drives another 20 km.
She again turns left and drives 40 km, then she turns to her right and drives for another 5 km. She again turns to her right and drives another 30 km to reach her bank where she works. What is the shortest distance between her bank and her house?
(a) 20 km
(b) 25 km
(c) 30 km
(d) 35 km
Correct Answer: (b) 25 km
Question from UPSC Prelims 2021 CSAT Paper
Explanation :
A bank employee drives 10 km south
Starting point: (0,0) – House
Movement sequence:
1. South 10 km → (0, -10)
2. Left turn, East 20 km → (20, -10)
3. Left turn, North 40 km → (20, 30)
4. Right turn, East 5 km → (25, 30)
5. Right turn, South 30 km → (25, 0) – Bank
Shortest distance calculation:
– Using Pythagorean theorem
– Distance = √[(x₂-x₁)² + (y₂-y₁)²]
– Distance = √[(25-0)² + (0-0)²]
– Distance = √(625 + 0)
– Distance = √625
– Distance = 25 km
Therefore, the shortest distance between her house and bank is 25 kilometers.