Q. In how many ways can a batsman score exactly 25 runs by scoring single runs, fours and sixes only, irrespective of the sequence of scoring shots ?

Explanation : 

In how many ways a batsman can score 25 runs ?

This problem can be solved by using the concept of integer solutions of an equation.

Let’s denote the number of singles as x, the number of fours as y, and the number of sixes as z. We are looking for the number of solutions to the equation:

x + 4y + 6z = 25

We also know that x, y, and z must be non-negative integers (since you can’t score a negative number of runs or a fraction of a run).

We can start by finding the maximum possible values for x, y, and z. The maximum value for x is 25 (if all runs are scored as singles), for y is 6 (if all runs are scored as fours), and for z is 4 (if all runs are scored as sixes).

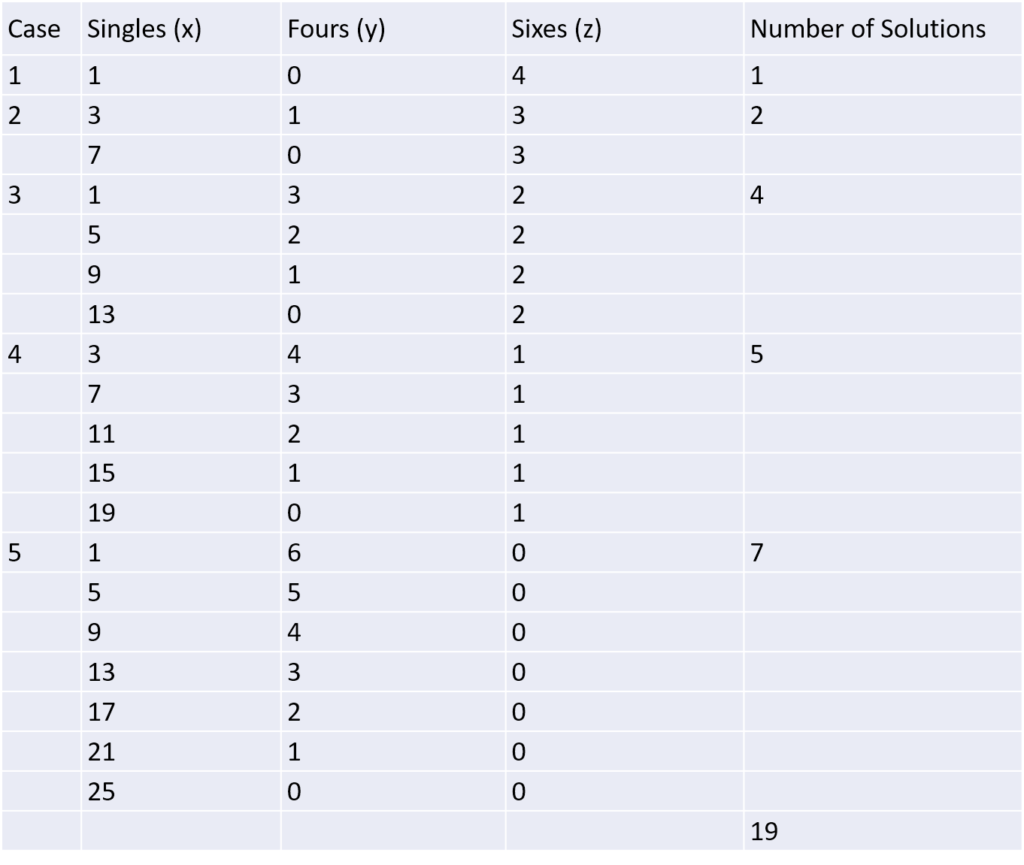
Now, we can start by assuming the maximum value for z and then find the possible values for y and x. If z = 4, then the remaining runs to be scored are 1, which can only be scored as a single. So, there is 1 solution in this case.

If z = 3, then the remaining runs to be scored are 7. These can be scored as 1 four and 3 singles, or 7 singles. So, there are 2 solutions in this case.

If z = 2, then the remaining runs to be scored are 13. These can be scored as 3 fours and 1 single, 2 fours and 5 singles, 1 four and 9 singles, or 13 singles. So, there are 4 solutions in this case.

If z = 1, then the remaining runs to be scored are 19. These can be scored as 4 fours and 3 singles, 3 fours and 7 singles, 2 fours and 11 singles, 1 four and 15 singles, or 19 singles. So, there are 5 solutions in this case.

If z = 0, then all runs must be scored as fours or singles. These can be scored as 6 fours and 1 single, 5 fours and 5 singles, 4 fours and 9 singles, 3 fours and 13 singles, 2 fours and 17 singles, 1 four and 21 singles, or 25 singles. So, there are 7 solutions in this case.

Adding up all these solutions, we get a total of 1 + 2 + 4 + 5 + 7 = 19 solutions. So, the answer is (b) 19.